目录
[TOC]
(一) 引例–GPS汽车导航
- GPS汽车导航:通过卫星来测量汽车的位置和速度。
- 由于测量误差的存在,你可能永远无法得知汽车的真实位置和速度。
- 此时,我们需要一种方法去估计汽车的位置和速度,让它更接近真实值。
- 特别是当误差较大时,算法显得尤为重要。
- 看看效果(代码在后面):
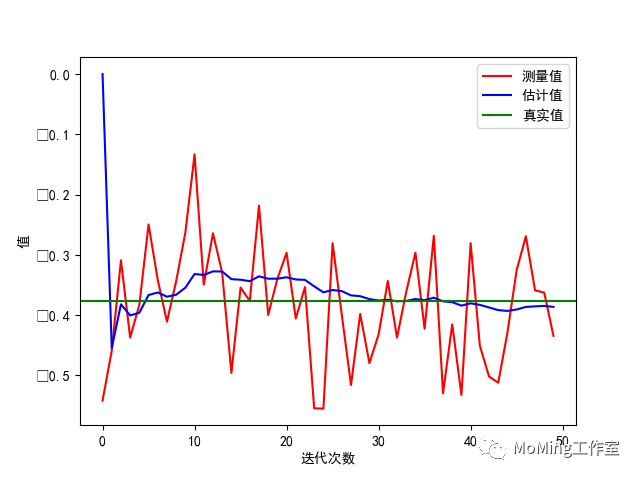
(二) 问题分析–无数学模型
- 待估计量不止1个,可以用列向量X表示。
- 这类问题是一个时域模型,以时间为自变量。估计量X=f(k)。
- 无法建立待估计量的数学模型。因为存在无法观察的数据量(地面坡度情况,开车习惯等)。
- 能获取的信息:观测值,测量传感器的误差。
(三) 解决方法–状态空间模型
无数学模型就用状态空间模型(这里因为卡尔曼滤波假设是线性模型),它用两个方程描述:
\[\left \{\begin{array}{l}
状态方程:X_k = AX_{k-1} + BU_{k-1} + W_{k-1} \\
测量方程:Z_k = HX_k + V_k \\
\end{array}\right.\]
- 状态方程:k时刻的状态X,可以从k-1时刻的状态+输入得出,同时考虑转移的过程误差W。
- A:状态转移矩阵。
- B:输入矩阵。
$X_{k-1}$:上一时刻的状态值向量。$U_{k-1}$:上一时刻的输入。$W_{k-1}$: 上一时刻的过程噪声。$X_k$:当前时刻的状态值向量。
- 测量方程:建立状态与观测值的关系,同时考虑观测误差V。
- H:输出矩阵
$X_k$:当前时刻的状态值向量。$V_k$: 当前时刻的测量噪声。$Z_k$:当前时刻的测量值向量。
- 状态空间模型特点:
- k时刻的状态只依赖k-1时刻的状态,不需要估计量的数学模型。
- 它是一个递归过程,从前一时刻状态得出当前状态。
- 不依赖很多历史数据,计算量小,占用内存小。
- 建立了状态与观测值的关系。
- W,V是噪音的,不确定则无法计算。
(四) 卡尔曼滤波,对状态空间模型的前提假设
- 假设是线性模型。才有上述两个方程。
- 假设W符合正态分布P(W)~(0,Q),期望是0,协方差是Q。
- 假设V符合正态分布P(V)~(0,R),期望是0,协方差是R。
- 假设估计值是真实值的无偏估计,且误差e符合正态分布P(e)~(0,P),期望是0,协方差是P。
(五) 卡尔曼滤波的五大公式(循环这五步进行计算)
- 数学符号
$$
\left {\begin{array}{l}
X_k: k时刻的真实值,是多个值组成的向量,永远无法知道\
Z_k: k时刻的观测值 \
\hat{X_k}: k时刻的X_k的估计值(也叫后验估计值,是经过校正的) \
\hat{X_k}^-: k时刻的X_k的先验估计值(忽略噪声直接算出来的) \
\hat{P_k}: k时刻的X_k的估计值与真实值的误差e_k服从的正态分布的协方差 \
\hat{P_k}^-: k时刻的X_k的先验估计\hat{X_k}^-与真实值X_k的误差e_k^-服从的正态分布的协方差 \
K_k: 卡尔曼增益系数 \
U,W,V等其他符号参考状态空间模型
\end{array}\right.
$$
-
提前准备的已知参数
\(\left \{\begin{array}{l}
A: 状态转移矩阵\\
B: 输入矩阵\\
H: 输出矩阵\\
Q: 正态分布P(W)的协方差矩阵,一维正态用均值方差描述,多维用协方差\\
R: 正态分布P(V)的协方差矩阵\\
(A,B, H, Q, R可动态变化)\\
\\
\hat{X}_0: 猜测的或者任意的估计初值\\
{P}_0: 猜测的或者任意的估计误差正态分布的协方差矩阵初值\\
\end{array}\right.\)
-
五个公式,也是五个步骤。(这里A,B,H下标都是k,省略)
\(预测:
\left \{\begin{array}{l}
\hat{X}_k^- = A\hat{X}_{k-1} + BU_{k-1} & (1) \\\\
P_k^- = A P_{k-1} A^T + Q_{k-1} & (2)
\end{array}\right.\)
\(校正:
\left \{\begin{array}{l}
K_k = P_k^- H^T (HP_k^-H^T + R_k)^{-1} & (3) \\ \\
\hat{X}_k = \hat{X}_k^- + K_k (Z_k - H\hat{X}_k^-) & (4) \\ \\
P_k = P_k^{-} - K_k H P_k^- & (5) \\
\end{array}\right.\)
- 五个公式解释:
- 公式(1): 从k-1时刻预测k时刻X的先验估计:线性计算。
- 公式(2): 从k-1时刻预测k时刻X的先验估计的误差协方差:跟转移误差Q有关。
- 公式(3): 计算卡尔曼增益系数:跟测量误差R有关。
- 公式(4): 数据融合,得到X的后验估计。
- 公式(5): 计算后验误差的协方差。
- 卡尔曼滤波的作用
- 滤波:估计真实值,降噪平滑。
- 预测:提前预测下一时刻的值
(六) python实现简单一维卡尔曼滤波
\[import numpy
import pylab
n_iter = 50 #计算次数
sz = (n_iter,)
#为了绘图,存放每次计算的值
xhat = numpy.zeros(sz) #x的估计值
P = numpy.zeros(sz) #x的估计值误差的协方差
xhatminus = numpy.zeros(sz) #x的先验估计
Pminus = numpy.zeros(sz) #x的先验估计值误差的协方差
K = numpy.zeros(sz) #x卡尔曼增益系数
#三个矩阵的假设,这里就直接忽略
#A=1
#B=0
#H=1
Q = 1e-5 #过程协方差
R = 0.1 ** 2 #测量误差协方差
#初值
xhat[0] = 0.0
P[0] = 1.0
x = -0.37727 #真实值
z = numpy.random.normal(x, 0.1, size=sz) #观测值
for k in range(1, n_iter):
#预测
xhatminus[k] = xhat[k - 1] #用公式(1),其中A=1,BU(k) = 0
Pminus[k] = P[k - 1] + Q #用公式(2),其中A=1,Q = 1e-5
#校正
K[k] = Pminus[k] / (Pminus[k] + R) #用公式(3),其中H=1,R=0.1**2
xhat[k] = xhatminus[k] + K[k] * (z[k] - xhatminus[k]) #用公式(4),其中H=1
P[k] = (1 - K[k]) * Pminus[k] #用公式(5),其中H=1
pylab.rcParams['font.sans-serif'] = ['SimHei'] #中文支持
pylab.figure()
pylab.plot(z, 'r-', label='测量值') #测量值
pylab.plot(xhat, 'b-', label='估计值') #后验估计值
pylab.axhline(x, color='g', label='真实值') #真实值
pylab.legend()
pylab.xlabel('迭代次数')
pylab.ylabel('值')\]
(七) 卡尔曼滤波的证明
- 出发点:融合理论。
- 用状态方程递推先验估计X1
- 用测量方程反算测量估计X2
- 那么估计值应该是两者的融合,即X的估计应该 = X1+G(X2-x1)。
- 为了方便,假设A,B, H, Q, R不变,对结果无影响。
- 证明五大公式:
- 用状态方程,先忽略过程误差算出先验估计,==得公式1==:
\(\hat{X}_k^- = A\hat{X}_{k-1} + BU_{k-1} \ \ \ (1)\)
- 用测量方程,先忽略测量误差V反算出测量估计:
\[\hat{X}_{kmeas} = H^{-1}Z_k\]
- 根据融合理论,后验估计值等于先验估计和测量估计的融合,==得公式4==:
\[\left \{\begin{array}{l}
\hat{X}_k = \hat{X}_k^- + G(\hat{X}_{kmeas} - \hat{X}_k^-)\\
\\
带入\hat{X}_{kmeas}得:\\
\hat{X}_k = \hat{X}_k^- + G( H^{-1}Z_k - \hat{X}_k^-) \\
\\
H^{-1}拿到括号外,整理一下得:\\
\hat{X}_k = \hat{X}_k^- + GH^{-1} (Z_k - H\hat{X}_k^-)\\
\\
令GH^{-1} = K_k 得公式4:\\
\hat{X}_k = \hat{X}_k^- + K_k (Z_k - H\hat{X}_k^-)\ \ \ \ (4)\\
\end{array}\right.\]
- 证明以及求解
$K_k$==得公式3==:
- 目标:寻找
$K_k$使得估计值$\hat{X}_k$最接近真实值$X_k$。
- 也就是要使得
$e_k$越接近均值0。也就是方差最小,也就是使得P的迹trace最小。
\[\left \{\begin{array}{l}
根据假设,e_k服从正态分布(0,P),均值为0,则:\\
期望E(e_i) = 0 ,这里省略时刻k,i是维度。\\
Cov(e_i,e_j) = E[(e_i-E(e_i)) (e_j-E(e_j)) ] = E(e_ie_j) \\
\\
P_k =
\left( \begin{matrix}
Cov(e_1,e_1) &Cov(e_1,e_2) &\cdots &Cov(e_1,e_n) \\
Cov(e_2,e_1) &Cov(e_2,e_2) &\cdots &Cov(e_2,e_n) \\
\vdots &\vdots &\ddots &\vdots \\
Cov(e_n,e_1) &Cov(e_n,e_2) &\cdots &Cov(e_n,e_n) \\
\end{matrix} \right) \\
= \left( \begin{matrix}
E(e_1,e_1) &E(e_1,e_2) &\cdots &E(e_1,e_n) \\
E(e_2,e_1) &E(e_2,e_2) &\cdots &E(e_2,e_n) \\
\vdots &\vdots &\ddots &\vdots \\
E(e_n,e_1) &E(e_n,e_2) &\cdots &E(e_n,e_n) \\
\end{matrix} \right) \\
= E(e e^T)\\
\\\\
其中 e_k = X_k - \hat{X}_k\\
由\\
\hat{X}_k = \hat{X}_k^- + K_k (Z(K) - H\hat{X}_k^- \\
Z_k = HX_k + V_k \\
代入e_k得:\\
e_k = X(k) - \hat{X}_k = X_k - \big(\hat{X}_k^- + K_k (Z(K) - H\hat{X}_k^-)\big) \\
= X_k - \hat{X}_k^- - K_kZ_k + K_kH\hat{X}_k^- \\
= X_k - \hat{X}_k^- - K_k\big( HX_k + V_k \big) + K_kH\hat{X}_k^- \\
= X_k - \hat{X}_k^- - K_kHX_k - K_kV_k + K_kH\hat{X}_k^- \\
= X_k - \hat{X}_k^- K_kH(X_k-\hat{X}_k^) - K_kV_k \\
= (I-K_kH)(X_k - \hat{X}_k^-) - K_kV_k \\
= (I-K_kH)e_k^- - K_kV_k \\
\\
P_k = E(e_k e_k^T) = E[(X(k) - \hat{X}_k) (X_k - \hat{X}_k)^T] \\
= E\big[ [(I-K_kH)e_k^- - K_kV_k] [(I-K_kH)e_k^- - K_kV_k]^T\big] \\
\\
由(AB)^T=B^TA^T,(A+B)^T=A^T+B^T得:\\
P_k = E\big[ [(I-K_kH)e_k^- - K_kV_k] [{e_k^-}^T(I-K_kH)^T - V_k^TK_k^T] \big] \\
= E\big[ (I-K_kH)e_k^-{e_k^-}^T(I-K_kH)^T - (I-K_kH)e_k^-V_k^TK_k^T - K_kV_k{e_k^-}^T(I-K_kH)^T + K_kV_kV_k^TK_k^T \big]\\
= E[(I-K_kH)e_k^-{e_k^-}^T(I-K_kH)^T] -E[(I-K_kH)e_k^-V_k^TK_k^T] -E[K_kV_k{e_k^-}^T(I-K_kH)^T] + E[K_kV_kV_k^TK_k^T] \\
\\
由e_k^-和V_k相互独立,可知E(e_k^-V_k) = 0,且E(e_k^-)= 0,E(V_k) = 0,E(V_k^T) = 0 得:\\
P_k = E[(I-K_kH)e_k^-{e_k^-}^T(I-K_kH)^T] + E[K_kV_kV_k^TK_k^T] \\
= (I-K_kH) E(e_k^-{e_k^-}^T) (I-K_kH)^T + K_k E(V_kV_k^T)K_k^T\\
= (I-K_kH) P_k^- (I-K_kH)^T + K_kRK_k^T \\
= (P_k^- - P_k^-K_kH)(I - H^TK_k^T) + K_kRK_k^T \\
= P_k^- -K_kHP_k^- - P_k^-H^TK_k^T + K_kHP_k^- H^TK_k^T + K_kRK_k^T \\
\\
下面求tr(P_k),P_k第二项的转置是第三项,则两项迹相等,得:\\
tr(P_k) = tr(P_k^-) - 2tr(K_kHP_k^-) + tr(K_kHP_k^- H^TK_k^T) + tr(K_kRK_k^T) \\
\\
求tr(P_k)最小值,对tr(P_k)求导\\
由\frac{d(tr(AB))}{dA} = B^T \\
由\frac{d(tr(ABA^T))}{dA} = 2AB \\
令 \frac{d(tr(P_k))}{dK_K} = 0 - 2(HP_k^-)^T + 2K_kHP_k^- H^T + 2K_kR = 0 得: \\
-(HP_k^-)^T + K_kHP_k^- H^T + K_kR = 0 \\
\\
由P_k^-是协方差对称矩阵得 \\
-P_k^-H^T + K_k(HP_k^- H^T + R) = 0 \\
K_k = \frac{P_k^-H^T}{HP_k^- H^T + R} \ \ \ (3)
\end{array}\right.\]
\[\left \{\begin{array}{l}
P_k^- = E[e_k^- {e_k^-}^T] \\\\
单独看e_k^-\\
e_k^- = X_k - \hat{X}_k^- \\
= A X_{k-1} + BU_{k-1} +W_{k-1} - A\hat{X}_{k-1} -BU_{k-1} \\
= A(X_{k-1} - \hat{X}_{k-1}) + W_{k-1} \\
= Ae_{k-1} + W_{k-1} \\
\\
带入到P_k^-得:\\
P_k^- = E[e_k^- {e_k^-}^T] \\
= E[( Ae_{k-1} + W_{k-1}) (Ae_{k-1} + W_{k-1})^T] \\
= E[( Ae_{k-1} + W_{k-1}) (e_{k-1}^TA^T + W_{k-1}^T)] \\
= E( Ae_{k-1}e_{k-1}^TA^T + Ae_{k-1}W_{k-1}^T + W_{k-1}e_{k-1}^TA^T + W_{k-1}W_{k-1}^T)) \\
\\
由e_{k-1}和W_{k-1}相互独立且期望为0得: \\
P_k^- = E( Ae_{k-1}e_{k-1}^TA^T + W_{k-1}W_{k-1}^T)\\
= AE(e_{k-1}e_{k-1}^T)A^T + E[W_{k-1}W_{k-1}^T]
= AP_{k-1}A^T + Q \ \ \ (2) \\
\end{array}\right.\]
\[\left \{\begin{array}{l}
由前面求K_k得知:\\
P_k = P_k^- -K_kHP_k^- - P_k^-H^TK_k^T + K_kHP_k^- H^TK_k^T + K_kRK_k^T\\
\\
整理下得:\\
P_k = P_k^- -K_kHP_k^- - P_k^-H^TK_k^T + K_k(HP_k^- H^T+R)K_k^T\\
\\
带入K_k得:\\
P_k = P_k^- -K_kHP_k^- - P_k^-H^TK_k^T + \frac{P_k^-H^T}{HP_k^- H^T + R}(HP_k^- H^T+R)K_k^T\\
\\
后面两项约掉:\\
P_k = P_k^- -K_kHP_k^-\\\\
提出P_k^-:\\
P_k= (I-K_kH)P_k^- \ \ \ \ (5)
\end{array}\right.\]
(八) 应用场景
- 无人机的飞行控制。
- 机器人运动控制。
- 加速度计和陀螺仪的角度估计。
- GPS/INS(GPS系统/惯性系统)的位置估计。
- 跟踪目标的大小,位置,速度估计。
- 传感器的真实值估计。
- WebRTC拥塞控制GCC算法的带宽估计。
- 数据的平滑。
(九) 扩展
- EKF(Extended Kalman Filter)
- UKF(Unscented Kalman Filter)
- AUKF (Augmented Unscented Kalman Filter)
(十) 参考
- 多维高斯分布与协方差矩阵
- 卡尔曼滤波器:https://www.bilibili.com/video/BV1ez4y1X7eR
- 状态空间模型:https://www.bilibili.com/video/BV1Az4y1d7nd
点击查看MoMing的分享笔记汇总